ECC: A Case for Mobile Encryption

Introduction:

It is needless to start this article by talking about the rise of mobile devices in the last few years. We all know how smart phones have swept the world. But with mobiles you always look for concepts or solutions that are computationally cheap. For example, Android OS uses a dex compiler to convert the Java bytecode to .dex files before compiling them. Why? Because dex files are optimized for low memory and low processing systems. Similarly, when it comes to encryption on mobile devices, we look for solutions that are computationally cheap and yet secure. ECC (elliptic curve cryptography) meets those requirements. This article explains why and how ECC is different from other types of encryption.

Learn Applied Cryptography

Build your applied cryptography and cryptanalysis skills with 13 courses covering hashing, PKI, SSL/TLS, full disk encryption and more.

Start Learning

What is the need for an alternative encryption scheme when you have RSA?

Mobile phones have two main limitations:

1. Computational limitations—The processors used on mobile devices are less capable than the ones used on a desktop system. Although there are a few devices that use dual core or quad core, most mobiles in general are not equipped with these kinds of CPUs.
2. Battery life—Mobile devices run throughout the day and low battery consumption is one of the important features needed for a device to be successful. The more computations a device has to perform, the more battery life is consumed.

Consider a normal user who visits a banking site on his mobile device to transfer money to his friend. A low processing-powered mobile device would struggle with the 1024-bit computations of RSA. With major financial institutions, the smallest key size allowed for RSA is 1024 bits. This activity not only takes time to complete, but it also eats into the battery life of the device.

What is ECC?

Elliptical curve cryptography (ECC) is a public key encryption technique based on elliptic curve theory that can be used to create faster, smaller, and more efficient cryptographic keys. So let us analyze the ECC algorithm by considering two factors, security and efficiency.

Security—When we talk about public key encryption algorithms, the first things that come to mind are RSA and Diffie-Hellman. Both these algorithms use 1024-bit keys for major transactions. But it's important here to note that NIST (National Institute for Standards and Technology) has recommended 1024-bit parameters only until the year 2010. The RSA algorithm is into its 40th birthday and probably regarded as the standard public key exchange on the Internet. After 2010, NIST believes that the existing systems should be upgraded to a different set up to provide more security (although we no longer believe NSA or NIST). One option is to simply increase the size of the key used with these algorithms. However, you are probably not quite sure what the safe key size is. Another option is to switch to a different setup that is more secure. ECC here comes to rescue. ECC generates keys through the properties of the elliptic curve equation instead of the traditional method of generation as the product of very large prime numbers.

RSA's security is based on the principle that factoring is slow and hard; i.e., it is difficult to factor a large integer composed of two or more large prime factors. With improvements in technology, the gap between factoring and multiplying is slowly shrinking. In the coming years, certainly this is bound to break. Switching to a larger key size is one option but it would only give the breathing space for a few more years.

An elliptic curve is represented as a looping line intersecting two axes. ECC is based on properties of a particular type of equation created from the mathematical group derived from points where the line intersects the axes. Multiplying a point on the curve by a number will produce another point on the curve, but it is very difficult to find what number was used, even if you know the original point and the result. For elliptic-curve-based protocols, it is assumed that finding the discrete logarithm of a random elliptic curve element with respect to a publicly known base point is not feasible—this is called the "elliptic curve discrete logarithm problem" or ECDLP. Equations based on elliptic curves have a characteristic that is very valuable for cryptography purposes: They are relatively easy to perform but extremely difficult to reverse. Despite almost three decades of research, mathematicians still haven't found an algorithm to solve this problem. To state it in simple words, for numbers of the same size, solving elliptic curve discrete logarithms is significantly very much harder than factoring. ECC was developed by Certicom, a mobile e-business security provider. RSA has been developing its own version of ECC. Other manufacturers, including Motorola, Cylink, Siemens, and VeriFone, etc., have already included support for ECC in their products.

The curious case of Angela Merkel's phone tapping

A few months back, the news that German Chancellor Angela Merkel's phone was tapped by the US government created quite a scene. Amid this controversy there was also news that Merkel used two phones, one a Blackberry (encrypted) and the other a Nokia (not encrypted). In September, new government phones that were manufactured by the Canadian company BlackBerry were delivered to all government officials (including Merkel) after being updated by the German company Secusmart. They contain a special encryption card that scrambles speech and data before transmitting it. This Secusmart card uses elliptic curve cryptography to encrypt and decrypt the mobile speech. But just because it is encrypted doesn't mean it's safe. It all depends upon how difficult it is to crack the key.

Efficiency—In terms of efficiency, ECC wins the race by large margin. The table below explains it all. The following table gives the key sizes recommended by the National Institute of Standards and Technology to protect keys used in conventional encryption algorithms like DES and AES, together with the key sizes for RSA, Diffie-Hellman, and elliptic curves that are needed to provide equivalent security.

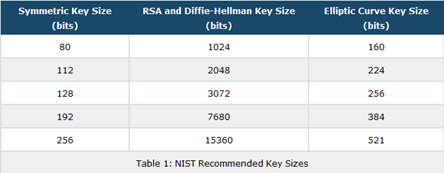
For instance, to protect 128-bit AES keys using RSA or Diffie-Hellman you need to use 3072-bit parameters. The equivalent key size for elliptic curves is only 256 bits. Also, as the symmetric key size increases, the corresponding RSA/Diffie Hellman key size increases at a much higher rate than the ECC key size. This is a particularly strong case for moving towards ECC for low-powered environments such as mobile devices, wireless devices, smart cards, etc.

Real-world ECC—is it safe?

The reports leaked by Edward Snowden suggested that dual elliptic curve deterministic random bit generation (or Dual_EC_DRBG) has been included as a NIST national standard due to the influence of NSA, which included a deliberate weakness in the algorithm and the recommended elliptic curve. RSA Security then issued an advisory recommending that its customers discontinue using any software based on Dual_EC_DRBG. Wikipedia mentions that "Implementations which used Dual_EC_DRBG would usually have gotten it via a library. At least RSA Security (BSAFE library), OpenSSL, Microsoft, and Cisco have libraries which included Dual_EC_DRBG, but only BSAFE used it by default. According to the Reuters article that revealed the secret $10 million deal between RSA Security and NSA, RSA Security's BSAFE was the most important distributor of the backdoor algorithm. There was a flaw in OpenSSL's implementation of Dual_EC_DRBG that made it non-working outside test mode, from which OpenSSL's Steve Marquess concludes that nobody used OpenSSL's Dual_EC_DRBG implementation." All these point out the dark side of the NSA J

However, there are several different standards that propose ways of selecting curves for use in elliptic-curve cryptography (ECC). Each of these standards tries to make sure that the elliptic-curve discrete-logarithm problem (ECDLP—the problem of finding an ECC user's secret key, given the user's public key) is difficult. Below are some of the standards in use:

• ANSI X9.62
• IEEE P136
• SEC 2
• NIST FIPS 186-2
• ANSI X9.63
• Brainpool
• NSA Suite B
• ANSSI FRP256V1

Hence, selecting the right curve and parameters is also important to ensure real world ECC security. More information can be found at the link: http://safecurves.cr.yp.to/.

To summarize:

Learn Applied Cryptography

Build your applied cryptography and cryptanalysis skills with 13 courses covering hashing, PKI, SSL/TLS, full disk encryption and more.

Start Learning

• ECC employs a relatively short encryption key. It is faster and requires less computing power than other first-generation encryption public key algorithms such as RSA and Diffie-Hellman. For example, a 160-bit ECC encryption key provides the same security as a 1024-bit RSA encryption key and can be up to 15 times faster, depending on the platform on which it is implemented.
• It is extremely helpful for use on low-memory and low-computing environments such as mobile devices, wireless devices, etc.
• Elliptic curves are supported by all modern browsers and most certification authorities offer elliptic curve certificates.

Elliptic curve cryptography has proven to be a promising solution for the implementation of public-key cryptosystems. As widespread use of the Internet and mobile devices continues to increase, transferring data with less computation and in a more secure manner has been the primary focus. With smaller key sizes and lower processing requirements, elliptic curve cryptography serves the purpose on mobile devices.